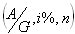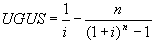problem and solve practice about equivalence and compound interest

1    .  Solve diagram a – d below for the uknown Q, R, S ant T, asumming a 10% interest rate. 

  answer:

1. 
   
2. 
   
3. 
   

Arithmetic Gradient

• The first cash flow is always equal to zero.
• A uniform increasing amount. 
• G = the difference between each cash amount.

A pure gradient (uniformly increasing amount) can also be converted into the equivalent present value of uniform series:

AG = G(A/G, i, n)

Example: The list price for a vehicle is stated as $25,000.  You are quoted a monthly payment of $658.25 per month for 4 years.  What is the monthly interest rate?  What interest rate would be quoted (yearly interest rate)?

Using factor table:

$25000 = $658.25(P/A,i,48)

 37.974 = (P/A,i,48)

 i = 1% from table 4, pg 705

 0r 12 % annually

Using formula:

Example: Find the number of periods required such that an invest of $1000 at 5% has a future worth of $5000.

  $P = $F(P/F,5%,n)

  $1000 = $5000(P/F,5%,n)

   .2 = (P/F,5%,n)

   n ~ 33 periods

Economics and uniform series formula

 

 

Note: Enter interest(i) in decimal form. For example, an interest rate of 15% would be entered as 0.15

Change Equation

Select an equation to solve for a different unknown

Discrete Compounding Discount Factors

		capital recovery
		single payment compound amount
		single payment present worth
		uniform gradient future worth
		uniform gradient present worth
		uniform gradient uniform series
		uniform series compound amount
		uniform series present worth
		uniform series sinking fund

example:

A Machine at a cost of $5,000 was purchased 3 years ago. It can be sold now for $3,000. If the machine is kept, the annual operating and maintenance costs will be $1,500. If it is kept and operated for next five years, determine the amount at time 0 (now) equivalent to the cost of owning and operating the machine can be sold for $1,000 at the end of the five year period. Use an interest rate of 10%.

A. 8065

B. 6550

C. 9522

D. 5002

solution:

F = P(1 + i)^n

F = A [((1 + i)^n - 1))/i]

P = A [((1 + i)^n - 1))/((i(1 + i)^n))]

P = $3,000

Operating and maintenance costs / year = $1,500

n = 5 years

Salvage value = $1,000

Interest rate = 10%

PW of costs = 3,000 + 1,500 (P/A, 10%, 5) - 1,000(P/F, 10%, 5)

= 3,000 + 1,500 (3.791) -1,000(0.6209)

= $8,065.60

The answer is, “A”.

  

Single payment formulas

Formula:

F = P(1+i)ⁿ

This is the single payment compound amount formula and is written in functional rotation as:

F = P(F/P, i, n)

P = F(P/F, i, n)

Example:

If $5000 were deposited in a bank saving account, how much would be in the account three years hence if the bank paid 6% interest compouded annually?

Solution:

We can draw a diagram of the problem. note: to have a consistent notation, we will represent receipt by upward arrows (and positive signs), and disbursement (or payment) will have downward arrows (and negative signs).

From the view point of the person depositing the $500, the diagram is:     

            

We need to identify the variuos elements of the equation. The presentsum P is $500. The interest period is 6%, and in three years are three interest periods. The future sum F is to be computed.

P = $500                        i=6%             n = 3                      F = unknown

F = P(1+i)ⁿ   =  500(1+0.06)³

=$ 595,50

If we deposit $500 in the bank now at 6% interest, there will be $595,50 in the account in three years.

Compound interest

To facilite equivalences computations, a series of interest formula will be derived. To simplify the presentation, we’ll use the following notation:

i =           interest rate per interest period. In the equation the interest rate is stated as a decimal (that is, 9%   minterest is 0.009).

n=           number of interest periods.

P =          a present sum of money

F =          A future sum of money. The future sum F is an amount, n interest periods from the present, that is ...equivalent to P with interest rate i.

A =         An end of period cash receipt or disbursement in a uniform series, continuing for n periods, the entire    ...series aquivalent to P or F at interest rate i.

Computing cash flows

In the examples presented so far, we have selected the least cost alternative to meet a specification or requirement or the saving have been obtained in a short period of time. There are other situations where the alternative have different consequences that continue for extended period of time.in these circumtances, we do not add up the various consequences; instead, describe aech alternative as cash receipts or disburshment at different points in  time. In this way, each alternative is revolve in to a cash flow.  This is the illustrated:

The manager has decide to purchase a new $30.000 mixing machine. The machine may be paid for by one of two ways:

1.       Pay the full price now minus a 3% discount.

2.       Pay $5000 now; at the end of one year, pay $8000; at the end of four subsequent years, pay $6000 per year.

List the alternatives in the form of a table of cash flows.

Solution:

In this problem, the two alternative represent different ways to pay for the mixing machine. While the firs plan represent a lump sum of $ 29.100 now, the second one call for payments continuing until the end of the fifth year. The problem is to convert an alternative in to cash receipts or disbursements and show the timing of each receipt or disbursement. The result called a cash flow table  or, more simply, a cash flow.

The cash flows for both the alternatives in this problem are very simple. The cash flo table, with disbursements given negative signs, is as follows:

End of year	Pay in full now	Pay over 5 years
0	-$29.100	-$5000
1	0	-8000
2	0	-6000
3	0	-6000
4	0	-6000
5	0	-6000

Decision making process

Decision making may take place by default, that is, whith out consciously recognizing that an opportunity for decision making exist. This fact leads us to a first elemen in a defenition of decisoin making. To have a decision making situation, there must be at least two alternatives avalaible.

Rational decision making:

We define the rational decision making process in terms of eight step:

1.       Recognition of a problem;

2.       Defenition of the goal or objective;

3.       Assembly of relevant data;

4.       Identification of feasible alternative;

5.       Selection of the criterion for judging which is the best alternative;

6.       Construction of the interrelationship between the objective, alternative, data and the criterion;

7.       Prediction of the outcomes for each alternative; and,

8.       Choice of the best alternatife to achive the objective.