Present value, also known as present discounted value, is the value on a given date of a payment or series of payments made at other times.
If the payments are in the future, they are discounted to reflect the time value of money and other factors such as investment risk. If they are in the past, their value is correspondingly enhanced to reflect that those payments have been (or could have been) earning interest in the intervening time. Present value calculations are widely used in business and economics to provide a means to compare cash flows at different times on a meaningful "like to like" basis.
Types of Economic Alternatives:
•Mutually Exclusive Alternatives:
–Only one of the viable projects can be
selected.
–The viable projects compete against one another.
–
•Independent Alternatives:
–More than one viable project may be
selected.
–There may be dependent projects requiring a particular project
to be selected before another.
–Contingent projects where one project may be substituted for
another.
Three criteria that apply to all
of our analysis techniques:
1.For fixed input situations, maximize the benefits or other outputs.
2.For fixed output situations, minimize the costs or other inputs.
3.Where inputs and outputs vary, maximize = benefits – costs.
Economic
Criteria Restated Present Worth Techniques
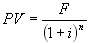
Change Equation
Select an equation to solve for a different unknown
present worth analysis
| present value or worth | |
| future value or worth | |
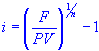 | interest rate |
present worth-annual payments
| present value or worth | |
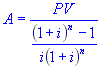 | annual payment or cost |
future value- annual payments
| annual payment or cost | |
| future value or worth |
example:
1.A new dam project will
require $48,000 a year in maintenance costs after it is complete. These
maintenance costs will continue forever. Assume that the funding can be set
aside in an account that earns 5% interest per year. What is the lump sum to be
set aside now in order to cover the $48,000 in annual maintenance costs?
The correct answer was: .
$960,000.
Solution: This is a
capitalized cost problem with an infinite analysis period.
Capitalized cost,
P= A/i
where A is the annual
disbursement and i is the interest rate.
P= $48,000/0.05
= $960,000. So,
$960,000 must be set aside in
this account in order to pay for annual maintenance costs.
2. Your grandfather
deposits $50,000 into your savings account that pays 6% interest compounded
quarterly. Equal annual withdrawals are to be made from the account beginning 1
year from now and continuing forever. The maximum amount of equal annual
withdrawals is approximately
The correct answer was:
$3,068.
Solution: First we need
to find the effective annual interest rate because our interest is compounded
quarterly instead of annually. We then use the effective annual interest in the
infinite life formula, P = A/i
Ie= (1+0.015)4 − 1 = 0.06136
The maximum annual withdrawal
is approximately A = Pi = 50,000(0.06136) = $3,068
3. Machine
A has an initial cost of $6,000 with total annual maintenance costs of $750.
Machine B has an initial cost of $8,500 with total annual maintenance costs of
$405. At a 10% interest rate, in approximately how many years do the two
machines have the same present worth?
The correct answer was: d. 10
years.
Solution: PW of cost A
= PW of cost B
6,000 + 750(P/A, 10%, n) =
8,500 + 405(P/A, 10%, n)
8,500 − 6,000 = 750 −
405(P/A, 10%, n)
(2,500/345) = (P/A, 10%,
n)
(P/A, 10%, n) = 7.25
So, from the 10% interest
table, this equates to about 10 years.
4. You borrow $10,000 from
your parents at an interest rate of 12% compounded monthly. You agree to pay
your parents $300 per month. Approximately how long will it take for you to pay
off your loan assuming that you pay exactly $300 per month?
The correct answer was: d. 41
months.
References: Solution: PW of
benefits = PW of costs
10,000 = 300(P/A, 1%,
n)
10,000/300 = (P/A, 1%,
n)
33.33 = (P/A, 1%, n)
n is approximately 41 months
references:

Tidak ada komentar:
Posting Komentar